Handles Near Inflection Node

Linus Romer

I did quite some mathematical investigation in "harmonizing" cubic Bézier curves. However, I am not sure how to handle the problem with handles near an inflection node. The following picture shall be an example of this problem (the blue areas are curvature combs):

The left S is a draft. The middle and the right S are possible improvements of the segments near the inflection nodes.

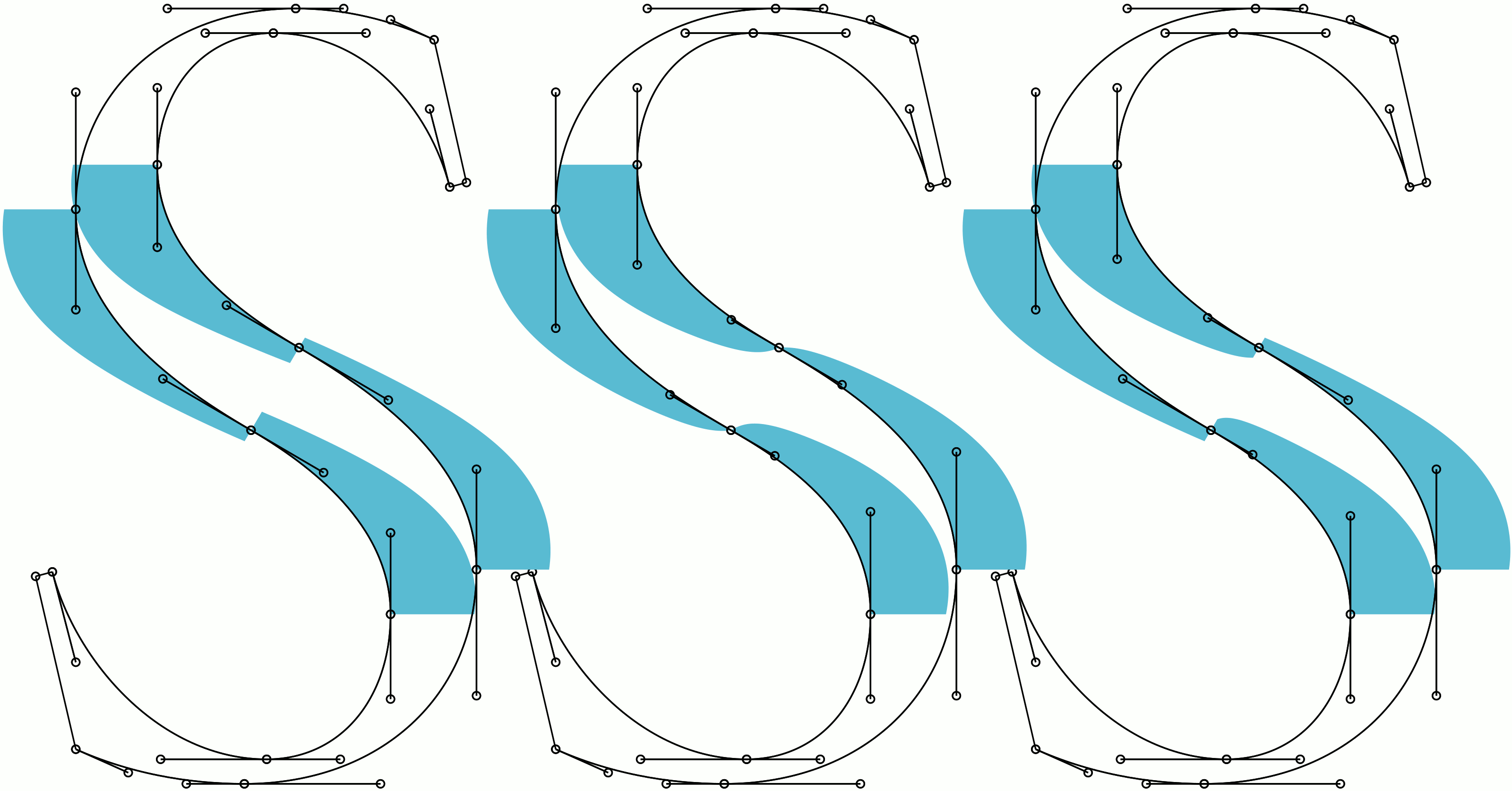
The problem with the draft (left) is, that the curvature changes abruptly. Now it would be mathematically advisable to change the handles such that the curvature in the inflection is 0 (mid). However, this means that the handles attached to the neighbour nodes have to reach exactely the intersection point of the node tangents - and this is critical for two reasons:

1. Rounding issue: After rounding, the handles may exceed the tangent triangle which means that an additional inflection point occurs on the segment.
2. Interpolation issue: Even if rounding is handled correctly, the same problem may occur after interpolation

Of course, one could remove the inflection node completely but this gives less control over the curve (less degree of freedom).

The S to the right changed the handles such that the curvature on both sides is the minimum of the curvature before on both sides. This is the best I could think of but it is an arbitrary choice. An other arbitrary choice could be to choose the technique in the middle but rescale the handles by e.g. 90%.

What choice would you recommend? («Use your eyes» is not a useful advice for me, because I need this for an algorithm).

Nick Shinn

I often put a short straight section in the middle of the S.

The straights can be shorter than in this example (Pratt Nova), of course.

Nick Curtis

I was going to suggest the same thing: it leaves fewer things to chance, and I used it often.

Jasper de Waard

While practically adding a straight piece in the middle may be great advice, I don't think it's what Linus is looking for (correct me if I'm wrong). It works because the start and end points of the straight piece are determined by the typedesigner, and there is no mathematical formula that could determine where those points should be for an optimally smooth curve. They are where they are, and that's that. However, that's also somewhat of a cop out. You avoid having to make a smooth curve, by making a curve that is intentionally non-smooth. You avoid fixing an essentially mathematical problem by replacing it with a 'curve' that cannot be optimized mathematically. It may work fine in many cases, but what if what I want is that smooth curve?

Regarding a different answer: I'm sorry. Haven't go a clue. But out of those S's, the middle one does look best.

Linus Romer

Indeed, the workaround solution with adding a short straight part is not what I have been looking for... Meanwhile, I have implemented the middle variant in Curvatura. This is visually and mathematically the best variant. It may require slight adjustions afterwards, but I think this is okay for most of the designers.

Jens Kutilek

In my updates on FF Hertz, I have added nodes at 45° to allow more control for width interpolations (I added new condensed and high-contrast masters), while keeping the curve around the inflection clear (of additional nodes).