Understanding the LeMo cadence grid

Simon Cozens

I'm trying to apply the cadence grid model from Notes on patterns and grids to help me space a new font; the results are turning out a bit strange so I want to check I understand it properly. Looking at that page, very near the bottom there's an example of an /n with its stem divided into 5 units. From that, we derive a 36 unit grid and spacing for all the Latin letters. I created a Glyphs plugin which divides the stem width into 5, sets up a grid, and so on. Then I set the sidebearings of my letters to the values given in the table. The result for light and normal weight Roman looks OK, but when we get into bold...



That seems... wrong. Is this expected? Does the cadence grid idea only apply for normal weights? Or have I misapplied something?

Here's an example of the bold /d fitting the grid - you can see we have two cadence units on the left and six on the right. That's right, isn't it?
 

(The shape and proportions of the glyph itself are a separate issue - this is My First Serif - I'm just looking at the sidebearings and the spacing at the moment.)

Simon Cozens

Frode Bo Helland said:

The space between letters is linked to the space inside them. Until you hit the beat, all you’ve got is a set of letterforms. When you find the rhythm, you’ve got yourself a typeface.

Good advice - but I should have been clearer about my question. It looks like I'm making a typeface, but actually I'm making a plugin...

My understanding is, yes: Frank’s units only apply to the regular weight romans.

Bother. But that's interesting, in two ways. First: I wonder if a similar table could be made for bolds? Second, it seems like Frank's system is agnostic of stem width, but it equally seems like it breaks down at larger stem widths. So maybe this means that the relationship between stem width and spacing does not scale as linearly (in the mathematical sense) as he suggests.

LeMo aka PatternMan aka Frank E Blokland

Hi Simon,

The cadencing works also fine for italics. It also works quite well for bold weights. At the moment I’m lecturing at the KABK and I will be traveling later today, but I will post some examples tomorrow. Perhaps Lukas Schneider is willing to show some examples generated with the LS Cadencer tool for RoboFont and Glyphs.

I would define the stem width in cadence units, like you can see in the image of Garamont’s Gros Canon Romain on top of the LeMo blog.

F.

Lukas Schneider

Hi Simon, 

the grid is flexible - so for bolder weights the steps of the grid can/will be increased.

See examples of Adobe Garamond spaced with LS Cadencer.
Lukas

PabloImpallari

Hi Simon, MekkaBlue developed a somewhat similar plugin for me a few weeks ago. I will release it on GitHub soon.

LeMo aka PatternMan aka Frank E Blokland

Hi Pablo, This makes me very curious! Best from a train, Frank

LeMo aka PatternMan aka Frank E Blokland

Brief introduction to the cadence-units concept –part 1




Measurements of Renaissance type matrices –as part of my PhD research– clearly prove that standardized character widths were used in the early days of typography. With the DTL LetterModeller (LeMo) application the relation between stem interval and the overshoot of curves can be simply demonstrated (see the two images above); the flattening of curves leaves the stem interval and hence the character widths unattached.



It is plausible that Jenson’s type was defined on a grid. It is possible that Jenson defined the x-height of his roman as five times the vertical stroke-width, i.e., stem thickness,  like calligraphers define the x-height of the Humanistic minuscule as five times the pen width. This unit system is rather course and it only works well for letters that share the archetypal proportions. As soon as one changes these proportions, things become more complex. For instance Van den Keere’s (Gros/Gras) Canon Romain (see image below), which seems to share the proportions of VdK’s rotunda Canon d’Espaigne, is clearly outside the archetypal model for roman type.



This effect can be reproduced with LeMo by ‘stretching’ some letters and by leaving other ones unattached. The rhythmical pattern is obstructed and the original mechanism does not provide a correct fitting. Such a deviation requires an adapted patterning.



In the image above the character width of the n is identical to that of the b, d, o, and p. In the image below only the widths of the n and m have been altered like in Van den Keere’s (Gros/Gras) Canon Romain



I distilled a system from especially French Renaissance type in which the stem interval (marked with ‘a’ in the image below) is divided into what I baptized cadence units. As a consequence the units are not by definition related anymore to the vertical stroke width, and subsequently the system becomes more versatile. These units are organic, i.e., distilled from the design itself still, however. This forms the basis for the parametrized cadence-units fitting.
        The cadence units are the result of a division of the stem interval of the lowercase letter n, indicated with ‘a’ in the image. The distance from a side bearing to the center of the n equals the stem interval. The resulting character width (twice as large as the stem interval) can be divided into smaller units by either bisecting aforenamed distance (which is the most logical method), or by dividing it in an arbitrary number of units. The cadence unit-arrangement system makes it possible to artificialy fit type.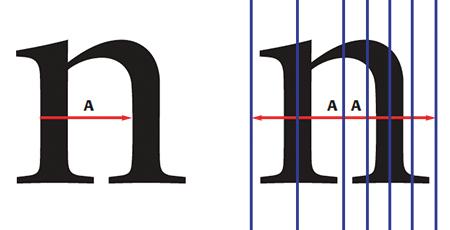


Cadence units are always font-specific. This in contrast with the units that are used in digital font tools, which are always universal. The resolution can be defined by the user and can be as refined as is preferred. However, the resolution does not have to be extremely high to generate a detailed spacing. That is one of the strengths of the system: a smaller design-related unit-arrangement system makes fitting easier to oversee and more controllable.
        If type is morphologically related, a comparable fitting system can be exchanged. The simplest way is to translate side-bearings distances into cadence units, and store these in a table. Because the size of these units is always font-specific, the units will become smaller or wider if the stem interval respectively decreases or increases. One can compare the effect with playing an accordion. The distances to the side bearings can be measured from stems or from extremes (curves or serifs). Distilled values can be listed and used for morphologically related typefaces, irrespective whether these are more condensed or wider than the archetypal model.

The table system is a simplification and a translation of a system of which was at the very base of roman and italic type. Initially a relatively simple pattern was required to control all aspects of the Renaissance type production, and to make the justifications of lines simpler. Later in history the system shifted to an optical interpretation of the early systematization and standardization. In the eightteenth century so-called set patterns (bundles of precast type for setting the registers of the mould) were delivered together with matrices which don't show the initial standardized widths. And then the stem-interval is not the dominant factor anymore, but the focus comes on the equilibrium of white space. And looking primarily (only?) at the white space in counters and between characters is what is taught in education nowadays.


        This equilibrium approach results by definition in an interruption of the stem interval if one does not take the latter into account. It is plausible that Jenson's asymmetric serifs, like the ones of the lowercase n, were meant to position the characters measurably centered in their widths. By shortening the serifs of the lower-case n at the left and enlarging them at the right, the weight was balanced at both sides and the side-bearings placed at equal distances form the stems. Nowadays type designers will for instance put somewhat more space at the left side of the i in comparison with the l.

LeMo aka PatternMan aka Frank E Blokland

Brief introduction to the cadence-units concept –part 2


The IKARUS-based program Kernus 3.0, developed by URW(++) calculates the space between characters based on a couple of key characters, like the lowercase n and o. It rasterizes the areas between characters and takes a couple of (exception) rules into account, like to prevent collisions between parts of different letters. Depending on the design, for instance the lengths of serifs can differ in basically identical situations, and subsequently the stem interval will be to some extent interrupted. As mentioned, for cadence-based fitting the stem interval forms the basis. The image above shows respectively DTL Fell with zero side-bearings, Kernus fitting and Kernagic (which uses the cadence-units system) fitting.


If a design clearly deviates from the archetypal models, like Comic Sans, then it looks obvious that trying to achieve an equilibrium of white space by (basically) purely calculating this, seems to make more sense than trying to distill (and subsequently apply) a cadenced-based fitting. However, the related test (see image above) shows a mixed result. Partly the Kernus approach provides better results and partly the Kernagic outcomes are preferable.
        The required relation to the archetypal font used for generating the list of values, implies that a font with for instance very flat curves requires more units from the extremes of these curves to the side bearings.





For defining the current Cadence Units Spacing Table (CUST) that come with the LS Cadencer tool a range of typefaces that can be considered archetypal was analyzed. In case of the Renaissance Roman [Regular] CUST (see below), Adobe Jenson, Adobe Garamond and DTL Haarlemmer formed the basis, and empirically the table was adjusted and subsequently fixed while applying it on a range of test fonts. For the Humanist Sans Roman [Regular] cust DTL Haarlemmer Sans was selected as archetypal font and for the Grotesk Roman [Regular] cust DTL Nobel. The current CUST versions are preliminary and no doubt the system will be improved over time.
        It should be mentioned here that for calculating the distances to the side bearings the grid is actually moved. The higher the resolution of the grid, the less this movement is necessary. the more one dilutes the table to more the grid becomes ‘universal’, i.e., applicable to every morphologically related font without the necessity to shift the units before applying them. In case of a 64-units grid for the stem-interval, stems and curves will fit within the grid. It should also mentioned that the grid system that seems to have been applied by Renaissance punch cutters is less refined than the ones used for cadencing. A grid with a relatively low resolution basically requires the adaptation of the design to the grid (which is not a bad idea anyway).
        The big advantage of the system is that the applied units are organic, i.e., distilled from the type itself. This in contrast with the digital grid for the em in which a present-day type designer normally designs and which is also used to define the fitting. Usually this is 1000 units or a multiple of this value, and this is unnecessarily refined for positioning the side bearings. At the end the cadence units are translated into the actual em units. This inevitably results in some rounding when the stem interval has to be divided into a certain number of units. Tests seem to prove that the tolerance is quite acceptable though. The alternative would be to adjust the stem interval to the grid.
        If a typeface is not deliberately designed on a cadence unit grid, then the system can be used for spacing still, as is proven by the fitting tests I made. By diluting the grid, the boundaries of the glyphs of such a typeface will fit in the grid eventually. So, a 64-unit grid will theoretically be even more universal, but the preliminary tests show not much differences in the outcomes with a 32-unit grid.

Even if one does the fitting optically, the auto-spacing (preferably) in combination with the display of the underlying pattern can help to improve matters. It provides a second opinion and one can compare one’s optical spacing with an approach which formed the basis for the conditioning of the type designer's eye. One can even adjust proportions to the distilled patterns.
        As mentioned, the CUST system works in such a way that the distilled units are font-specific. For applying a CUST the proportions do not have to be exactly identical to the archetypal ones used for defining the table; as long as the morphology is related the system will work. The ‘Renaissance roman’ CUST below is for use in the LS Cadencer tool. ‘X’ means extreem on th x-axis and ‘S’ means stem. So in case of the capital A, units are applied at both sides from the extremes.


Cadence Units Spacing Table
Renaissance Roman [Regular–Bold]
Version 0.2
n_basis 32

'A_XX': ['2', '2'],
'B_SX': ['14', '6'],
'C_XX': ['7', '7'],
'D_SX': ['14', '7'],
'E_SX': ['14', '5'],
'F_SX': ['14', '2'],
'G_XS': ['7', '14'],
'H_SS': ['14', '14'],
'I_SS': ['14', '14'],
'J_SS': ['14', '12'],
'K_SX': ['14', '1'],
'L_SX': ['14', '4'],
'M_SS': ['14', '14'],
'N_SS': ['14', '12'],
'O_XX': ['7', '7'],
'P_SX': ['14', '3'],
'Q_XX': ['7', '7'],
'R_SX': ['14', '1'],
'S_XX': ['6', '7'],
'T_XX': ['1', '1'],
'U_SS': ['11', '11'],
'V_XX': ['1', '1'],
'W_XX': ['1', '1'],
'X_XX': ['2', '2'],
'Y_XX': ['1', '1'],
'Z_XX': ['5', '6'],
'a_XS': ['5', '10'],
'b_SX': ['9', '4'],
'c_XX': ['4', '1'],
'colon_XX': ['7', '7'],
'comma_XX': ['6', '7'],
'd_XS': ['4', '10'],
'e_XX': ['4', '3'],
'f_SX': ['11', '1'],
'g_XX': ['5', '1'],
'h_SS': ['10', '10'],
'i_SS': ['11', '10'],
'j_SS': ['10', '9'],
'k_SX': ['10', '0'],
'l_SS': ['10', '10'],
'm_SS': ['11', '10'],
'n_SS': ['11', '10'],
'o_XX': ['4', '4'],
'p_SX': ['10', '4'],
'period_XX': ['7', '7'],
'q_XS': ['4', '9'],
'r_SX': ['11', '0'],
's_XX': ['4', '4'],
'semicolon_XX': ['7', '7'],
't_SX': ['9', '1'],
'u_SS': ['10', '11'],
'v_XX': ['0', '0'],
'w_XX': ['0', '0'],
'x_XX': ['0', '0'],
'y_XX': ['0', '0'],
'z_XX': ['4', '4']

LeMo aka PatternMan aka Frank E Blokland

Brief introduction to the cadence-units concept –part 3


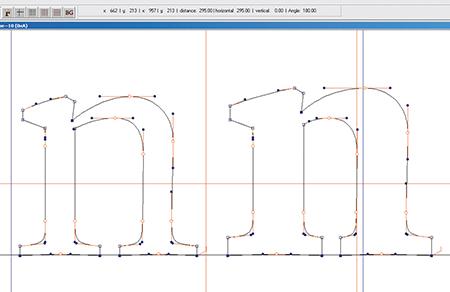
Bold weights are deviations from the original pattern of roman type, which was initially, i.e., in the fifteenth century, only meant for the ‘regular’ weight. One can approach the bold weights in two ways: with a specifically adapted table representing the narrower counters and hence the small distances to the side bearings in comparison with the regular weight, or by adapting the same table as is used for the regular weight, taking into account that the bold weight is a variant of the regular one. In the latter case the same unit-values can be used as for the regular weight if the size of the units is decreased.



Basically italic (or cursive) variants can be handled the same way as roman type, i.e., using a specific table based on archetypal models. However, this requires a more precise point of measurement of the stems. Another matter that has to be taken into account is the angle of the italics, which can differ quite a bit. When it comes to shape, roughly two archetypal models can be traced: the Italian Renaissance italic (think of Arrighi) with its basically interrupted construction and the French Renaissance cusrive (think of Granjon, Guyot) with its basically uninterrupted construction and rounder shapes.

Michael Vokits

Cripes, this is brilliant stuff... how about sans faces? I have got to get a font editor that supports scripting and plugins.

LeMo aka PatternMan aka Frank E Blokland

... how about sans faces?

No problemo. The original fitting of Monotype’s Gill Sans looks like this:

And the cadenced version looks like this:

There is some inelegant rounding in the screen dumps, so I will post PDF’s a.s.a.p.

Michael Vokits

“Dude, did you just punch out Cthulhu?”

Bravo!

LeMo aka PatternMan aka Frank E Blokland

Hi Pablo,

Hi Simon, MekkaBlue developed a somewhat similar plugin for me a few weeks ago. I will release it on GitHub soon.

I saw this nice YouTube presentation today. Nice! Just curious: you named it ‘a somewhat similar plugin’ when Lukas showed some of his LS Cadencer outcomes. To what extent is it similar? I noticed that Walter Tracy is mentioned in the credits.

Tracy’s system differs from mine because the basis is optical per font and subsequently the distances to the side bearings are used for other related shapes. The basic idea of cadence units is that if the morphology of a typeface is related to that of the archetypal models, the same spacing method –translated into fixed numbers of cadence units (which are by definition font specific)– can be applied. Hence the spacing defined in units can be used across typefaces.

In Letters of Credit Tracy advises to space the lowercase n and o first. ‘When the two letters look well regulated they are measured against the units gauge and the widths of the letters and their side spaces modified so as to maintain the ideal balance of black to white.’ Referring to the side bearings of the n and the o Tracy provides a scheme with relative values for the spacing of the other characters. A couple of letters, namely the S, a, f, g, s, t, and z fall outside this scheme and ‘[…] must be spaced visually, between standards.’† How were these exceptions handled by the macro?

*Walter Tracy, Letters of Credit (Boston, 1986) p.75.

†ibid.

PabloImpallari

Hi Frank, those are two separate things.
My macro is just a simple helper that shows some guidelines in the background to make working with unitized typefaces easier, it doesn't do the spacing for you.
The video is Andres Torresi's wonderful auto-spacing macro.

Ramiro Espinoza

I installed Kernagic but the lack of a proper tutorial made the experience of using it quite frustrating. Also: The "Cadence" method is not present in the current version. It looks like it has been renamed as "Table based" method.

Michael Vokits

Kernagic is nifty, but yes, it can be quite frustrating.

The first issue was getting it; I got it from github and compiled it myself, so I was a) in for a world of hurt with Mingw (until I decided to use a pure 32-bit toolchain) and b) on an obsolete version anyway. Found b2, works without a hitch.

I’m with Ramiro on the usage; maybe I’m just too fond of RTFM? No matter; it’s less complex than it seems.

Why it moves /i so far to the left is beyond me; the table is correct. Probably because I left it as a SEAC reference to /dotlessi and /dotaccent... yep, ‘tis the cause.

However, I think my real issue with kernagic is that it doesn’t allow for negative spacing; what to do with /f? Easy enough to space afterwards (especially since it depends on the length of the arm), but still, doing so makes me feel dirty and hubristic – LeMo can punch out Cthulhu (Gillthulhu?), but I’m, ah, a wee bit less able than they.

I’d love to see italic cadences... does anybody have any?